Movimiento parabólico
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico. En la superficie de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente podemos calcular su trayectoria usando la ecuación matemática de una parábola. La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire, la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de la Tierra sí tendríamos que utilizar una elipse(como en el caso de los satélites artificiales).
El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
El tiro parabólico tiene las siguientes características:
- Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales.
- La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
- Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
- Se puede analizar el movimiento en vertical independientemente del horizontal.
Tipos de movimiento parabólico
Movimiento parabólico (completo)
El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
- Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
- La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
- Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
- El tiempo que tarda en alcanzar su altura máxima es el mismo tiempo que tarda en recorrer la mitad de su distancia horizontal, es decir, el tiempo total necesario para alcanzar la altura máxima y regresar al suelo es el mismo para el total de recorrido horizontal.
Ecuaciones del movimiento parabólico
Hay dos ecuaciones que rigen el movimiento parabólico: es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad. son dos versores (vectores unitarios) en el plano.
son dos versores (vectores unitarios) en el plano.
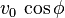 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.
- En lo sucesivo

- En lo sucesivo
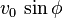 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
- En lo sucesivo
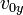
- En lo sucesivo
 : [ecu. 1]
: [ecu. 1]
Ecuación de la aceleración
La única aceleración que interviene en este movimiento es la constante de la gravedad, que corresponde a la ecuación:Ecuación de la velocidad
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
| [mostrar]
Deducción de la ecuación de la velocidad
|
|---|
Ecuación de la posición
Partiendo de la ecuación que establece la velocidad del móvil con la relación al tiempo y de la definición de velocidad, la posición puede ser encontrada integrando de la siguiente ecuación diferencial:La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
| [mostrar]
Deducción de las ecuación de la posición
|
|---|
Movimiento parabólico con rozamiento
Cuando consideramos el rozamiento la trayectoria es casi una parábola pero no exactamente. El estudio de la trayectoria en ese caso es considerado por la balística.Generalizaciones relativistas
En teoría de la relatividad para que un móvil ejecute una trayectoria parabólica se requiere un campo de fuerzas no uniforme o una fuerza dependiente del tiempo. Sin embargo, es interesante estudiar un análogo aproximado que sería el de un móvil sometido a una fuerza constante que no sea paralela a la velocidad, esto ocasiona un movimiento cuasiparabólico. Este es, por ejemplo, con gran aproximación el movimiento que ejecuta un electrón u otra partícula cargada frente a una placa plana cargada uniformemente (condensador plano). La ecuación de movimiento relativista para el movimiento bajo una fuerza constante, alineada con la dirección X es:Donde w es una constante que, para valores pequeños de la velocidad comparados con la velocidad de la luz, es aproximadamente igual a la aceleración (para velocidades cercanas a la de la luz la aceleración es mucho más pequeña que el cociente entre la fuerza y la masa).




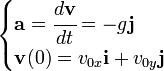

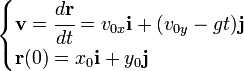


Este comentario ha sido eliminado por el autor.
ResponderEliminarla información no me sirbe
ResponderEliminarNo hay
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarNo me sirvió ni vrg
ResponderEliminarsi me sirve
ResponderEliminar