Movimiento circular
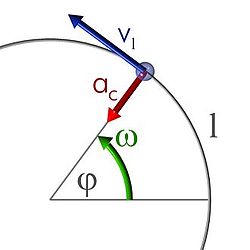
En cinemática, el movimiento circular (también llamado movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de giro es constante (giro ondulatorio), se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio y centro fijos y velocidad angular constante.
Movimiento circular.
Conceptos
En el movimiento circular hay que tener en cuenta algunos conceptos que serían básicos para la descripción cinemática y dinámica del mismo:- Eje de giro: es la línea recta alrededor de la cual se realiza la rotación, este eje puede permanecer fijo o variar con el tiempo pero para cada instante concreto es el eje de la rotación (considerando en este caso una variación infinitesimal o diferencial de tiempo). El eje de giro define un punto llamado centro de giro de la trayectoria descrita (O).
- Arco: partiendo de un centro fijo o eje de giro fijo, es el espacio recorrido en la trayectoria circular o arco de radio unitario con el que se mide el desplazamiento angular. Su unidad es el radián (espacio recorrido dividido entre el radio de la trayectoria seguida, división de longitud entre longitud, adimensional por tanto).
- Velocidad angular: es la variación del desplazamiento angular por unidad de tiempo (omega minúscula,
 ).
). - Aceleración angular: es la variación de la velocidad angular por unidad de tiempo (alfa minúscula,
 ).
).
- Momento angular (L): es la magnitud que en el movimiento rectilíneo equivale al momento lineal o cantidad de movimiento pero aplicada al movimiento curvilíneo, circular y/o giratorio (producto vectorial de la cantidad de movimiento por el vector posición, desde el centro de giro al punto donde se encuentra la masa puntual).
- Momento de inercia (I): es una cualidad de los cuerpos que depende de su forma y de la distribución de su masa y que resulta de multiplicar una porción concreta de la masa por la distancia que la separa al eje de giro.
- Momento de fuerza (M): o par motor es la fuerza aplicada por la distancia al eje de giro (es el equivalente a la fuerza agente del movimiento que cambia el estado de un movimiento rectilíneo).
Paralelismo entre el movimiento rectilíneo y el movimiento circular
| Lineal | Angular |
|---|---|
| Posición | Arco |
| Velocidad | Velocidad angular |
| Aceleración | Aceleración angular |
| Masa | Momento de inercia |
| Fuerza | Momento de fuerza |
| Momento lineal | Momento angular |
Arco descrito o desplazamiento angular
Arco angular o desplazamiento angular es el arco de la circunferencia recorrido por la masa puntual en su trayectoria circular, medido en radianes y representado con la letras griegas (phi) o
(phi) o  (theta). Este arco es el desplazamiento efectuado en el movimiento circular y se obtiene mediante la posición angular (
(theta). Este arco es el desplazamiento efectuado en el movimiento circular y se obtiene mediante la posición angular ( ó
ó  ) en la que se encuentra en un momento determinado el móvil y al que se le asocia un ángulo determinado en radianes. Así el arco angular o desplazamiento angular se determinará por la variación de la posición angular entre dos momentos final e inicial concretos (dos posiciones distintas):
) en la que se encuentra en un momento determinado el móvil y al que se le asocia un ángulo determinado en radianes. Así el arco angular o desplazamiento angular se determinará por la variación de la posición angular entre dos momentos final e inicial concretos (dos posiciones distintas):Siendo
 ó
ó 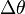 el arco angular o desplazamiento angular dado en radianes.
el arco angular o desplazamiento angular dado en radianes.Si se le llama
 al espacio recorrido a lo largo de la trayectoria curvilínea de la circunferencia de radio
al espacio recorrido a lo largo de la trayectoria curvilínea de la circunferencia de radio  se tiene que es el producto del radio de la trayectoria circular por la variación de la posición angular (desplazamiento angular):
se tiene que es el producto del radio de la trayectoria circular por la variación de la posición angular (desplazamiento angular):En ocasiones se denomina
 al espacio recorrido (del inglés "space"). Nótese que al multiplicar el radio por el ángulo
en radianes, al ser estos últimos adimensionales (arco entre radio), el
resultado es el espacio recorrido en unidades de longitud elegidas para
expresar el radio.
al espacio recorrido (del inglés "space"). Nótese que al multiplicar el radio por el ángulo
en radianes, al ser estos últimos adimensionales (arco entre radio), el
resultado es el espacio recorrido en unidades de longitud elegidas para
expresar el radio.Velocidad angular y velocidad tangencial
- Velocidad angular es la variación del arco angular o posición angular respecto al tiempo. Es representada con la letra
 (omega minúscula) y viene definida como:
(omega minúscula) y viene definida como:
Siendo la segunda ecuación la de la velocidad angular instantánea (derivada de la posición angular con respecto del tiempo).
- Velocidad tangencial
de la partícula es la velocidad del objeto en un instante de tiempo
(magnitud vectorial con módulo, dirección y sentido determinados en ese
instante estudiado). Puede calcularse a partir de la velocidad angular.
Si
 es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
Aceleración angular y tangencial
La aceleración angular es la variación de la velocidad angular por unidad de tiempo y se representa con la letra: y se la calcula:
y se la calcula:Si at es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:
Período y frecuencia
El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo. Se mide en hercios o s-1
Aceleración y fuerza centrípeta
Mecánica clásica
La aceleración centrípeta, también llamada normal o radial, afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. Se define como:La fuerza centrípeta es la fuerza que produce en la partícula la aceleración centrípeta. Dada la masa del móvil, y basándose en la segunda ley de Newton (
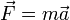 ) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:
) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:Mecánica relativista
En mecánica clásica la aceleración y la fuerza en un movimiento circular siempre son vectores paralelos, debido a la forma concreta que toma la segunda ley de Newton. Sin embargo, en relatividad especial la aceleración y la fuerza en un movimiento circular no son vectores paralelos a menos que se trate de un movimiento circular uniforme. Si el ángulo formado por la velocidad en un momento dado es entonces el ángulo
entonces el ángulo  formado por la fuerza y la aceleración es:
formado por la fuerza y la aceleración es:Para el movimiento rectilineo se tiene que
 y por tanto
y por tanto  y para el movimiento circular uniforme se tiene
y para el movimiento circular uniforme se tiene  y por tanto también
y por tanto también  . En el resto de casos
. En el resto de casos  . Para velocidades muy pequeñas y ángulos expresados en radianes se tiene:
. Para velocidades muy pequeñas y ángulos expresados en radianes se tiene:
Movimiento circular
En cinemática, el movimiento circular (también llamado movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de giro es constante (giro ondulatorio), se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio y centro fijos y velocidad angular constante.

Movimiento circular.Conceptos
En el movimiento circular hay que tener en cuenta algunos conceptos que serían básicos para la descripción cinemática y dinámica del mismo:
En dinámica de los movimientos curvilíneos, circulares y/o giratorios se tienen en cuenta además las siguientes magnitudes:
- Eje de giro: es la línea recta alrededor de la cual se realiza la rotación, este eje puede permanecer fijo o variar con el tiempo pero para cada instante concreto es el eje de la rotación (considerando en este caso una variación infinitesimal o diferencial de tiempo). El eje de giro define un punto llamado centro de giro de la trayectoria descrita (O).
- Arco: partiendo de un centro fijo o eje de giro fijo, es el espacio recorrido en la trayectoria circular o arco de radio unitario con el que se mide el desplazamiento angular. Su unidad es el radián (espacio recorrido dividido entre el radio de la trayectoria seguida, división de longitud entre longitud, adimensional por tanto).
- Velocidad angular: es la variación del desplazamiento angular por unidad de tiempo (omega minúscula,
).
- Aceleración angular: es la variación de la velocidad angular por unidad de tiempo (alfa minúscula,
).
- Momento angular (L): es la magnitud que en el movimiento rectilíneo equivale al momento lineal o cantidad de movimiento pero aplicada al movimiento curvilíneo, circular y/o giratorio (producto vectorial de la cantidad de movimiento por el vector posición, desde el centro de giro al punto donde se encuentra la masa puntual).
- Momento de inercia (I): es una cualidad de los cuerpos que depende de su forma y de la distribución de su masa y que resulta de multiplicar una porción concreta de la masa por la distancia que la separa al eje de giro.
- Momento de fuerza (M): o par motor es la fuerza aplicada por la distancia al eje de giro (es el equivalente a la fuerza agente del movimiento que cambia el estado de un movimiento rectilíneo).
Paralelismo entre el movimiento rectilíneo y el movimiento circular
A pesar de las diferencias evidentes en su trayectoria, hay ciertas similitudes entre el movimiento rectilíneo y el circular que deben mencionarse y que resaltan las similitudes y equivalencias de conceptos y un paralelismo en las magnitudes utilizadas para describirlos. Dado un eje de giro y la posición de una partícula puntual en movimiento circular o giratorio, para una variación de tiempo Δt o un instante dt, dado, se tiene:
Movimiento Lineal Angular Posición Arco Velocidad Velocidad angular Aceleración Aceleración angular Masa Momento de inercia Fuerza Momento de fuerza Momento lineal Momento angular
Arco descrito o desplazamiento angular
Arco angular o desplazamiento angular es el arco de la circunferencia recorrido por la masa puntual en su trayectoria circular, medido en radianes y representado con la letras griegas(phi) o
(theta). Este arco es el desplazamiento efectuado en el movimiento circular y se obtiene mediante la posición angular (
ó
) en la que se encuentra en un momento determinado el móvil y al que se le asocia un ángulo determinado en radianes. Así el arco angular o desplazamiento angular se determinará por la variación de la posición angular entre dos momentos final e inicial concretos (dos posiciones distintas):
Siendoó
el arco angular o desplazamiento angular dado en radianes.
Si se le llamaal espacio recorrido a lo largo de la trayectoria curvilínea de la circunferencia de radio
se tiene que es el producto del radio de la trayectoria circular por la variación de la posición angular (desplazamiento angular):
En ocasiones se denominaal espacio recorrido (del inglés "space"). Nótese que al multiplicar el radio por el ángulo en radianes, al ser estos últimos adimensionales (arco entre radio), el resultado es el espacio recorrido en unidades de longitud elegidas para expresar el radio.
Velocidad angular y velocidad tangencial
- Velocidad angular es la variación del arco angular o posición angular respecto al tiempo. Es representada con la letra
(omega minúscula) y viene definida como:
Siendo la segunda ecuación la de la velocidad angular instantánea (derivada de la posición angular con respecto del tiempo).
- Velocidad tangencial de la partícula es la velocidad del objeto en un instante de tiempo (magnitud vectorial con módulo, dirección y sentido determinados en ese instante estudiado). Puede calcularse a partir de la velocidad angular. Si
es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
Aceleración angular y tangencial
La aceleración angular es la variación de la velocidad angular por unidad de tiempo y se representa con la letra:y se la calcula:
Si at es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:
Período y frecuencia
El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:
La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo. Se mide en hercios o s-1
Aceleración y fuerza centrípeta
Mecánica clásica
La aceleración centrípeta, también llamada normal o radial, afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. Se define como:
La fuerza centrípeta es la fuerza que produce en la partícula la aceleración centrípeta. Dada la masa del móvil, y basándose en la segunda ley de Newton () se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:
Mecánica relativista
En mecánica clásica la aceleración y la fuerza en un movimiento circular siempre son vectores paralelos, debido a la forma concreta que toma la segunda ley de Newton. Sin embargo, en relatividad especial la aceleración y la fuerza en un movimiento circular no son vectores paralelos a menos que se trate de un movimiento circular uniforme. Si el ángulo formado por la velocidad en un momento dado esentonces el ángulo
formado por la fuerza y la aceleración es:
Para el movimiento rectilineo se tiene quey por tanto
y para el movimiento circular uniforme se tiene
y por tanto también
. En el resto de casos
. Para velocidades muy pequeñas y ángulos expresados en radianes se tiene:


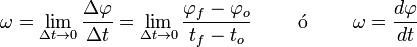
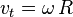
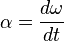




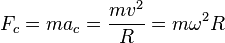


No hay comentarios:
Publicar un comentario