Movimiento armónico simple
El movimiento armónico simple (m.a.s.), también denominado movimiento vibratorio armónico simple (m.v.a.s.), es un movimiento periódico, y vibratorio en ausencia de fricción, producido por la acción de una fuerza recuperadora que es directamente proporcional a la posición. Y que queda descrito en función del tiempo por una función senoidal (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s.En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.

Movimiento armónico simple, mostrado en el espacio real y en el espacio fásico. Las órbita es periódica.
Mecánica clásica
Cinemática del movimiento armónico simple
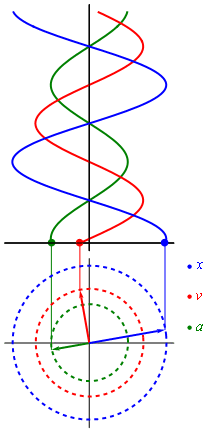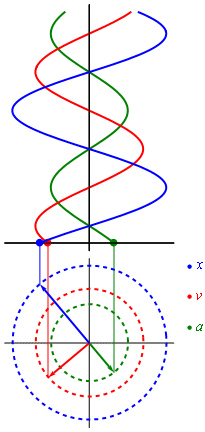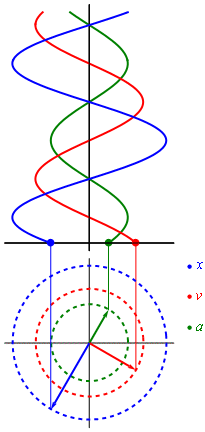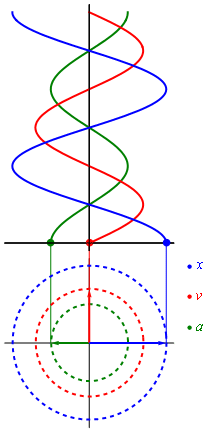
Evolución en el tiempo del desplazamiento, la velocidad y la aceleración en un movimiento circular uniforme.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo.El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
 donde
donde  es una constante positiva y
es una constante positiva y  es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).
es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial
Siendo
 la masa del cuerpo en desplazamiento. Escribiendo
la masa del cuerpo en desplazamiento. Escribiendo 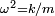 se obtiene la siguiente ecuación donde
se obtiene la siguiente ecuación donde  es la frecuencia angular del movimiento:
es la frecuencia angular del movimiento:(2)La solución de la ecuación diferencial () puede escribirse en la forma
(3)donde:
 es la elongación o desplazamiento respecto al punto de equilibrio.
es la elongación o desplazamiento respecto al punto de equilibrio. es la amplitud del movimiento (elongación máxima).
es la amplitud del movimiento (elongación máxima). es la frecuencia angular
es la frecuencia angular es el tiempo.
es el tiempo. es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
(4)La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión, y por lo tanto el periodo como
 .
.Velocidad
La velocidad instantánea de un punto material que ejecuta un movimiento armónico simple se obtiene por lo tanto derivando la posición respecto al tiempo:(5)
Aceleración
La aceleración es la variación de la velocidad del movimiento respecto al tiempo de espera y se obtiene por lo tanto derivado la ecuación de la velocidad respecto al tiempo de encuentro:(6)
Amplitud y fase inicial
La amplitud y la fase inicial
y la fase inicial  se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación
se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación  y de la velocidad
y de la velocidad  iniciales.
iniciales.(7)
(8)Sumando miembro a miembro las dos ecuaciones () y () obtenemos
(9)Dividiendo miembro a miembro las dos ecuaciones () y () obtenemos
(10)
Dinámica del movimiento armónico simple
En el movimiento armónico simple la fuerza que actúa sobre el móvil es directamente proporcional:(11)Un ejemplo sería el que realiza un objeto unido al extremo un muelle, en ese caso k sería la constante de elasticidad del muelle. Aplicando la segunda ley de newton tendríamos:
(12)Comparando esta ecuación y la que teníamos para la aceleración () se deduce:
(13)Esta ecuación nos permite expresar el periodo (T) del movimiento armónico simple en función de la masa de la partícula y de la constante elástica de la fuerza que actúa sobre ella:
(14)
Energía del movimiento armónico simple
(15)La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
(18)Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos
 y
y  . Se obtiene entonces que,
. Se obtiene entonces que,(19)O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio

(20)
Ejemplos
Medición de masa en ingravidez
En condiciones de ingravidez no es posible medir la masa de un cuerpo a partir de su peso. Sin embargo, se puede recurrir al principio del movimiento armónico simple para realizar tal medición.Para ello se instaló en la estación espacial Skylab un dispositivo (experimento M1721 ) destinado a medir la masa de los tripulantes consistente en una silla oscilante capaz de medir su periodo de oscilación
 electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:
electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:(21)
Mecánica relativista y mecánica cuántica
En mecánica relativista el análogo del movimiento armónico simple, es un movimiento en el que la fuerza es proporcional a la elongación pero debido a las peculiaridades de la teoría de la relatividad el movimiento resultante es sólo cuasiarmónico, y no exactamente armónico. En mecánica cuántica no puede hablarse propiamente de trayectorias, pero existe también un análogo cuántico de dicho movimiento.Mecánica relativista
El problema del oscilador en mecánica relativista no admite una solución analítica simple debido a que la ecuación del movimiento implica integrar la siguiente ecuación:2Sin embargo, puede una solución aproximada con las condiciones de contorno
 dada por:2
dada por:2donde:
Mecánica cuántica
Por lo que por lo expuesto anteriormente el espectro de posibles energías de la partícula será puramente puntual (es decir, será una combinación de funciones de niveles energéticos separados). Los posibles valores de la energía son:
y las funciones de onda asociadas son:
donde
 son los polinomios de Hermite.
son los polinomios de Hermite.Mecánica clásica
Cinemática del movimiento armónico simple

Evolución en el tiempo del desplazamiento, la velocidad y la aceleración en un movimiento circular uniforme.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo.El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
 donde
donde  es una constante positiva y
es una constante positiva y  es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).
es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial
Siendo
 la masa del cuerpo en desplazamiento. Escribiendo
la masa del cuerpo en desplazamiento. Escribiendo 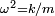 se obtiene la siguiente ecuación donde
se obtiene la siguiente ecuación donde  es la frecuencia angular del movimiento:
es la frecuencia angular del movimiento:(2)La solución de la ecuación diferencial () puede escribirse en la forma
(3)donde:
 es la elongación o desplazamiento respecto al punto de equilibrio.
es la elongación o desplazamiento respecto al punto de equilibrio. es la amplitud del movimiento (elongación máxima).
es la amplitud del movimiento (elongación máxima). es la frecuencia angular
es la frecuencia angular es el tiempo.
es el tiempo. es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
(4)La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión, y por lo tanto el periodo como
 .
.Velocidad
La velocidad instantánea de un punto material que ejecuta un movimiento armónico simple se obtiene por lo tanto derivando la posición respecto al tiempo:(5)
Aceleración
La aceleración es la variación de la velocidad del movimiento respecto al tiempo de espera y se obtiene por lo tanto derivado la ecuación de la velocidad respecto al tiempo de encuentro:(6)
Amplitud y fase inicial
La amplitud y la fase inicial
y la fase inicial  se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación
se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación  y de la velocidad
y de la velocidad  iniciales.
iniciales.(7)
(8)Sumando miembro a miembro las dos ecuaciones () y () obtenemos
(9)Dividiendo miembro a miembro las dos ecuaciones () y () obtenemos
(10)
Dinámica del movimiento armónico simple
En el movimiento armónico simple la fuerza que actúa sobre el móvil es directamente proporcional:(11)Un ejemplo sería el que realiza un objeto unido al extremo un muelle, en ese caso k sería la constante de elasticidad del muelle. Aplicando la segunda ley de newton tendríamos:
(12)Comparando esta ecuación y la que teníamos para la aceleración () se deduce:
(13)Esta ecuación nos permite expresar el periodo (T) del movimiento armónico simple en función de la masa de la partícula y de la constante elástica de la fuerza que actúa sobre ella:
(14)
Energía del movimiento armónico simple
(15)La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
(18)Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos
 y
y  . Se obtiene entonces que,
. Se obtiene entonces que,(19)O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio

(20)
Ejemplos
Medición de masa en ingravidez
En condiciones de ingravidez no es posible medir la masa de un cuerpo a partir de su peso. Sin embargo, se puede recurrir al principio del movimiento armónico simple para realizar tal medición.Para ello se instaló en la estación espacial Skylab un dispositivo (experimento M1721 ) destinado a medir la masa de los tripulantes consistente en una silla oscilante capaz de medir su periodo de oscilación
 electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:
electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:(21)
Mecánica relativista y mecánica cuántica
En mecánica relativista el análogo del movimiento armónico simple, es un movimiento en el que la fuerza es proporcional a la elongación pero debido a las peculiaridades de la teoría de la relatividad el movimiento resultante es sólo cuasiarmónico, y no exactamente armónico. En mecánica cuántica no puede hablarse propiamente de trayectorias, pero existe también un análogo cuántico de dicho movimiento.Mecánica relativista
El problema del oscilador en mecánica relativista no admite una solución analítica simple debido a que la ecuación del movimiento implica integrar la siguiente ecuación:2Sin embargo, puede una solución aproximada con las condiciones de contorno
 dada por:2
dada por:2donde:
Mecánica cuántica
Por lo que por lo expuesto anteriormente el espectro de posibles energías de la partícula será puramente puntual (es decir, será una combinación de funciones de niveles energéticos separados). Los posibles valores de la energía son:
y las funciones de onda asociadas son:
donde
 son los polinomios de Hermite.
son los polinomios de Hermite.Mecánica clásica
Cinemática del movimiento armónico simple

Evolución en el tiempo del desplazamiento, la velocidad y la aceleración en un movimiento circular uniforme.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo.El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
 donde
donde  es una constante positiva y
es una constante positiva y  es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).
es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial
Siendo
 la masa del cuerpo en desplazamiento. Escribiendo
la masa del cuerpo en desplazamiento. Escribiendo 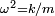 se obtiene la siguiente ecuación donde
se obtiene la siguiente ecuación donde  es la frecuencia angular del movimiento:
es la frecuencia angular del movimiento:(2)La solución de la ecuación diferencial () puede escribirse en la forma
(3)donde:
 es la elongación o desplazamiento respecto al punto de equilibrio.
es la elongación o desplazamiento respecto al punto de equilibrio. es la amplitud del movimiento (elongación máxima).
es la amplitud del movimiento (elongación máxima). es la frecuencia angular
es la frecuencia angular es el tiempo.
es el tiempo. es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
(4)La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión, y por lo tanto el periodo como
 .
.Velocidad
La velocidad instantánea de un punto material que ejecuta un movimiento armónico simple se obtiene por lo tanto derivando la posición respecto al tiempo:(5)
Aceleración
La aceleración es la variación de la velocidad del movimiento respecto al tiempo de espera y se obtiene por lo tanto derivado la ecuación de la velocidad respecto al tiempo de encuentro:(6)
Amplitud y fase inicial
La amplitud y la fase inicial
y la fase inicial  se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación
se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación  y de la velocidad
y de la velocidad  iniciales.
iniciales.(7)
(8)Sumando miembro a miembro las dos ecuaciones () y () obtenemos
(9)Dividiendo miembro a miembro las dos ecuaciones () y () obtenemos
(10)
Dinámica del movimiento armónico simple
En el movimiento armónico simple la fuerza que actúa sobre el móvil es directamente proporcional:(11)Un ejemplo sería el que realiza un objeto unido al extremo un muelle, en ese caso k sería la constante de elasticidad del muelle. Aplicando la segunda ley de newton tendríamos:
(12)Comparando esta ecuación y la que teníamos para la aceleración () se deduce:
(13)Esta ecuación nos permite expresar el periodo (T) del movimiento armónico simple en función de la masa de la partícula y de la constante elástica de la fuerza que actúa sobre ella:
(14)
Energía del movimiento armónico simple
(15)La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
(18)Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos
 y
y  . Se obtiene entonces que,
. Se obtiene entonces que,(19)O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio

(20)
Ejemplos
Medición de masa en ingravidez
En condiciones de ingravidez no es posible medir la masa de un cuerpo a partir de su peso. Sin embargo, se puede recurrir al principio del movimiento armónico simple para realizar tal medición.Para ello se instaló en la estación espacial Skylab un dispositivo (experimento M1721 ) destinado a medir la masa de los tripulantes consistente en una silla oscilante capaz de medir su periodo de oscilación
 electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:
electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:(21)
Mecánica relativista y mecánica cuántica
En mecánica relativista el análogo del movimiento armónico simple, es un movimiento en el que la fuerza es proporcional a la elongación pero debido a las peculiaridades de la teoría de la relatividad el movimiento resultante es sólo cuasiarmónico, y no exactamente armónico. En mecánica cuántica no puede hablarse propiamente de trayectorias, pero existe también un análogo cuántico de dicho movimiento.Mecánica relativista
El problema del oscilador en mecánica relativista no admite una solución analítica simple debido a que la ecuación del movimiento implica integrar la siguiente ecuación:2Sin embargo, puede una solución aproximada con las condiciones de contorno
 dada por:2
dada por:2donde:
Mecánica cuántica
Por lo que por lo expuesto anteriormente el espectro de posibles energías de la partícula será puramente puntual (es decir, será una combinación de funciones de niveles energéticos separados). Los posibles valores de la energía son:
y las funciones de onda asociadas son:
donde
 son los polinomios de Hermite.
son los polinomios de Hermite.Mecánica clásica
Cinemática del movimiento armónico simple

Evolución en el tiempo del desplazamiento, la velocidad y la aceleración en un movimiento circular uniforme.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo.El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
 donde
donde  es una constante positiva y
es una constante positiva y  es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).
es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial
Siendo
 la masa del cuerpo en desplazamiento. Escribiendo
la masa del cuerpo en desplazamiento. Escribiendo 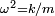 se obtiene la siguiente ecuación donde
se obtiene la siguiente ecuación donde  es la frecuencia angular del movimiento:
es la frecuencia angular del movimiento:(2)La solución de la ecuación diferencial () puede escribirse en la forma
(3)donde:
 es la elongación o desplazamiento respecto al punto de equilibrio.
es la elongación o desplazamiento respecto al punto de equilibrio. es la amplitud del movimiento (elongación máxima).
es la amplitud del movimiento (elongación máxima). es la frecuencia angular
es la frecuencia angular es el tiempo.
es el tiempo. es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
(4)La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión, y por lo tanto el periodo como
 .
.Velocidad
La velocidad instantánea de un punto material que ejecuta un movimiento armónico simple se obtiene por lo tanto derivando la posición respecto al tiempo:(5)
Aceleración
La aceleración es la variación de la velocidad del movimiento respecto al tiempo de espera y se obtiene por lo tanto derivado la ecuación de la velocidad respecto al tiempo de encuentro:(6)
Amplitud y fase inicial
La amplitud y la fase inicial
y la fase inicial  se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación
se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación  y de la velocidad
y de la velocidad  iniciales.
iniciales.(7)
(8)Sumando miembro a miembro las dos ecuaciones () y () obtenemos
(9)Dividiendo miembro a miembro las dos ecuaciones () y () obtenemos
(10)
Dinámica del movimiento armónico simple
En el movimiento armónico simple la fuerza que actúa sobre el móvil es directamente proporcional:(11)Un ejemplo sería el que realiza un objeto unido al extremo un muelle, en ese caso k sería la constante de elasticidad del muelle. Aplicando la segunda ley de newton tendríamos:
(12)Comparando esta ecuación y la que teníamos para la aceleración () se deduce:
(13)Esta ecuación nos permite expresar el periodo (T) del movimiento armónico simple en función de la masa de la partícula y de la constante elástica de la fuerza que actúa sobre ella:
(14)
Energía del movimiento armónico simple
(15)La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
(18)Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos
 y
y  . Se obtiene entonces que,
. Se obtiene entonces que,(19)O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio

(20)
Ejemplos
Medición de masa en ingravidez
En condiciones de ingravidez no es posible medir la masa de un cuerpo a partir de su peso. Sin embargo, se puede recurrir al principio del movimiento armónico simple para realizar tal medición.Para ello se instaló en la estación espacial Skylab un dispositivo (experimento M1721 ) destinado a medir la masa de los tripulantes consistente en una silla oscilante capaz de medir su periodo de oscilación
 electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:
electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:(21)
Mecánica relativista y mecánica cuántica
En mecánica relativista el análogo del movimiento armónico simple, es un movimiento en el que la fuerza es proporcional a la elongación pero debido a las peculiaridades de la teoría de la relatividad el movimiento resultante es sólo cuasiarmónico, y no exactamente armónico. En mecánica cuántica no puede hablarse propiamente de trayectorias, pero existe también un análogo cuántico de dicho movimiento.Mecánica relativista
El problema del oscilador en mecánica relativista no admite una solución analítica simple debido a que la ecuación del movimiento implica integrar la siguiente ecuación:2Sin embargo, puede una solución aproximada con las condiciones de contorno
 dada por:2
dada por:2donde:
Mecánica cuántica
Por lo que por lo expuesto anteriormente el espectro de posibles energías de la partícula será puramente puntual (es decir, será una combinación de funciones de niveles energéticos separados). Los posibles valores de la energía son:
y las funciones de onda asociadas son:
donde
 son los polinomios de Hermite.
son los polinomios de Hermite.Mecánica clásica
Cinemática del movimiento armónico simple

Evolución en el tiempo del desplazamiento, la velocidad y la aceleración en un movimiento circular uniforme.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo.El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
 donde
donde  es una constante positiva y
es una constante positiva y  es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).
es la elongación. El signo negativo indica que en todo momento la
fuerza que actúa sobre la partícula está dirigida hacía la posición de
equilibrio; esto es, en dirección contraria a su elongación (la "atrae"
hacia la posición de equilibrio).Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial
Siendo
 la masa del cuerpo en desplazamiento. Escribiendo
la masa del cuerpo en desplazamiento. Escribiendo 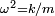 se obtiene la siguiente ecuación donde
se obtiene la siguiente ecuación donde  es la frecuencia angular del movimiento:
es la frecuencia angular del movimiento:(2)La solución de la ecuación diferencial () puede escribirse en la forma
(3)donde:
 es la elongación o desplazamiento respecto al punto de equilibrio.
es la elongación o desplazamiento respecto al punto de equilibrio. es la amplitud del movimiento (elongación máxima).
es la amplitud del movimiento (elongación máxima). es la frecuencia angular
es la frecuencia angular es el tiempo.
es el tiempo. es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
(4)La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión, y por lo tanto el periodo como
 .
.Velocidad
La velocidad instantánea de un punto material que ejecuta un movimiento armónico simple se obtiene por lo tanto derivando la posición respecto al tiempo:(5)
Aceleración
La aceleración es la variación de la velocidad del movimiento respecto al tiempo de espera y se obtiene por lo tanto derivado la ecuación de la velocidad respecto al tiempo de encuentro:(6)
Amplitud y fase inicial
La amplitud y la fase inicial
y la fase inicial  se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación
se pueden calcular a partir de las condiciones iniciales del movimiento, esto es de los valores de la elongación  y de la velocidad
y de la velocidad  iniciales.
iniciales.(7)
(8)Sumando miembro a miembro las dos ecuaciones () y () obtenemos
(9)Dividiendo miembro a miembro las dos ecuaciones () y () obtenemos
(10)
Dinámica del movimiento armónico simple
En el movimiento armónico simple la fuerza que actúa sobre el móvil es directamente proporcional:(11)Un ejemplo sería el que realiza un objeto unido al extremo un muelle, en ese caso k sería la constante de elasticidad del muelle. Aplicando la segunda ley de newton tendríamos:
(12)Comparando esta ecuación y la que teníamos para la aceleración () se deduce:
(13)Esta ecuación nos permite expresar el periodo (T) del movimiento armónico simple en función de la masa de la partícula y de la constante elástica de la fuerza que actúa sobre ella:
(14)
Energía del movimiento armónico simple
(15)La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
(18)Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos
 y
y  . Se obtiene entonces que,
. Se obtiene entonces que,(19)O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio

(20)
Ejemplos
Medición de masa en ingravidez
En condiciones de ingravidez no es posible medir la masa de un cuerpo a partir de su peso. Sin embargo, se puede recurrir al principio del movimiento armónico simple para realizar tal medición.Para ello se instaló en la estación espacial Skylab un dispositivo (experimento M1721 ) destinado a medir la masa de los tripulantes consistente en una silla oscilante capaz de medir su periodo de oscilación
 electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:
electrónicamente. A partir de este dato, y conociendo la constante de
fuerza del resorte unido a la silla, es posible entonces calcular la
masa del individuo:(21)
Mecánica relativista y mecánica cuántica
En mecánica relativista el análogo del movimiento armónico simple, es un movimiento en el que la fuerza es proporcional a la elongación pero debido a las peculiaridades de la teoría de la relatividad el movimiento resultante es sólo cuasiarmónico, y no exactamente armónico. En mecánica cuántica no puede hablarse propiamente de trayectorias, pero existe también un análogo cuántico de dicho movimiento.Mecánica relativista
El problema del oscilador en mecánica relativista no admite una solución analítica simple debido a que la ecuación del movimiento implica integrar la siguiente ecuación:2Sin embargo, puede una solución aproximada con las condiciones de contorno
 dada por:2
dada por:2donde:
Mecánica cuántica
Por lo que por lo expuesto anteriormente el espectro de posibles energías de la partícula será puramente puntual (es decir, será una combinación de funciones de niveles energéticos separados). Los posibles valores de la energía son:
y las funciones de onda asociadas son:
donde
 son los polinomios de Hermite.
son los polinomios de Hermite.







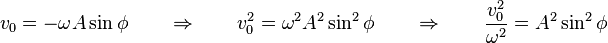



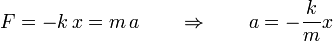

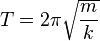



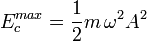

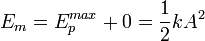
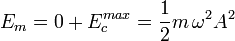

![\frac{\mathrm{d}^2 x}{\mathrm{d}t^2}
\left[ 1 - \left(\frac{1}{c} \frac{\mathrm{d} x}{\mathrm{d}t} \right)^2 \right]^{-3/2} =
-\frac{k}{m}x](https://upload.wikimedia.org/math/c/0/4/c0461c5e45601f60f55162e8610f8173.png)




 . El eje horizontal muestra la posición y en unidades (h/2πmω)1/2. Las gráficas están sin normalizar.
. El eje horizontal muestra la posición y en unidades (h/2πmω)1/2. Las gráficas están sin normalizar.

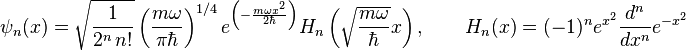
No hay comentarios:
Publicar un comentario