Mecánica del sólido rígido

La mecánica de un sólido rígido es aquella que estudia el movimiento y equilibrio de sólidos materiales ignorando sus deformaciones. Se trata, por tanto, de un modelo matemático útil para estudiar una parte de la mecánica de sólidos, ya que todos los sólidos reales son deformables. Se entiende por sólido rígido un conjunto de puntos del espacio que se mueven de tal manera que no se alteran las distancias entre ellos, sea cual sea la fuerza actuante (matemáticamente, el movimiento de un sólido rígido viene dado por un grupo uniparamétrico de isometrías).

Movimiento complejo de un sólido rígido, que presenta precesión alrededor de la dirección del momento angular además rotación según su eje de simetría

Cinemática del sólido rígido

Centro de gravedad

El centro de gravedad o centro de masas de un sistema continuo es el punto geométrico definido como:

(1) $\mathbf r_\text{CM} = \frac{\int\mathbf r dm}{\int dm} = \frac{\int\mathbf r dm}{M}$

En mecánica del sólido rígido, el centro de masa se usa porque tomando un sistema de coordenadas centrado en él, la energía cinética total K puede expresarse como

\scriptstyle{K={1\over2}MV^2+K_{rot}}

, siendo M la masa total del cuerpo, V la velocidad de traslación del centro de masas y K_rot la energía de rotación del cuerpo, expresable en términos de la velocidad angular y el tensor de inercia.

Velocidad angular

Sea una partícula cualquiera de un sólido rígido el cual se desplaza girando. Dado que todos los puntos están rígidamente conectados podemos hacer la siguiente descomposición de posición y velocidades, tomando un punto de referencia arbitrario

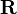\mathbf{r}_0

(2a) $\mathbf{r}(t,\mathbf{r}_0) = \mathbf{r}_c(t) + \mathbf{r} (t,\mathbf{r}_0) = \mathbf{r}_c(t) + A(t) \mathbf{r}_0$

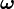(2b) $\mathbf{v}(t,\mathbf{r}_0) = \mathbf{v}_c(t) + \boldsymbol\omega(t) \times \mathbf{R}(t,\mathbf{r}_0) = \mathbf{v}_c(t) + \boldsymbol\omega(t) \times (\mathbf{r}(t,\mathbf{r}_0) - \mathbf{y}_c(t)) = \mathbf{v}_c(t) + \boldsymbol\omega(t) \times A(t) \mathbf{y}_0$

(2c) $A'(t)\mathbf{r}_0 = \boldsymbol\omega(t) \times A(t)\mathbf{y}_0$

Donde

$\mathbf{r}$ es vector posición del punto o partícula
$\mathbf{r}_c$ es la posición de un punto de referencia del sólido
$A(t)\in SO(3)$ es la orientación, que viene dada por una matriz ortogonal
$\mathbf{R}$ es la posición de la partícula con respecto al punto de referencia del cuerpo a lo largo del tiempo con una orientación variable.
$\mathbf{r}_0$ es la posición de la partícula con respecto al punto de referencia del cuerpo en la orientación de referencia inicial.
$\boldsymbol\omega$ es la velocidad angular
$\mathbf{v}$ es la velocidad total de la partícula
$\mathbf{v}_c$ es la velocidad "traslacional" o velocidad del punto de referencia.

Momento angular o cinético

Artículo principal: Momento angular

El momento angular es una magnitud física importante porque en muchos sistemas físicos constituye una magnitud conservada, a la cual bajo ciertas condiciones sobre las fuerzas es posible asociarle una ley de conservación. El hecho de que el momento angular sea bajo ciertas circunstancias una magnitud cuyo valor permanece constante puede ser aprovechado en la resolución de las ecuaciones de movimiento. En un instante dado, y fijado un punto del espacio en un punto del espacio O, se define el momento angular L_O de un sistema de partículas respecto a ese punto como la integral siguiente:

\mathbf{L}_O = \int_V \rho(\mathbf{r}_O\times\mathbf{v}_O) \quad dV

Donde

V, \rho(\mathbf{r})

son el volumen del sólido y la densidad másica en cada punto, y

\mathbf{v}_O, \mathbf{r}_O

son la velocidad de una partícula del cuerpo y el vector de posición respecto a O. Conviene recordar que el valor de la magnitud anterior depende de qué punto O se elija. Para el estudio de sólidos rígidos en movimiento conviene escoger un "punto móvil" (es decir, para cada instante del tiempo consideraremos un punto diferente del espacio). Por ejemplo podemos evaluar el momento angular respecto al centro de masas G del sólido:

(3)

$\mathbf{v}_G = \boldsymbol\omega\times\mathbf{r}$
$\mathbf{L}_G = \int_V \rho\left[\mathbf{r}\times(\boldsymbol\omega\times\mathbf{r})\right]dV = \int_V \rho\left[(\mathbf{r}\cdot\mathbf{r})\boldsymbol\omega -\mathbf{r}(\mathbf{r}\cdot\boldsymbol\omega)\right] dV$

Donde se ha introducido la abreviación

\mathbf{r} = \mathbf{r}_G

Espacio de configuración de un sólido rígido

La mecánica lagrangiana para describir un sistema mecánico con un grado finito de grados de libertad se define como una variedad diferenciable llamada espacio de configuración. El movimiento del sistema o evolución con el tiempo se describe como un conjunto de trayectorias a lo largo del espacio de configuración. Para un sólido rígido con un punto inmóvil (sólo existe rotación) el espacio de configuración viene dado por la variedad diferenciable del grupo de rotación SO(3). Cuando el sólido tiene traslación y rotación de todos sus puntos el espacio de configuración es E⁺(n), el subgrupo de isometría del grupo euclídeo (combinaciones de traslaciones y rotaciones.

Tensor de inercia

Artículo principal: Tensor de inercia

Cuando se estudia el movimiento de un sólido rígido resulta conveniente descomponerlo en un movimiento de traslación más un movimiento de rotación:

Para describir la traslación sólo necesitamos calcular las fuerzas resultantes y aplicar las leyes de Newton como si se tratara de puntos materiales.
En cambio la descripción de la rotación es más compleja, ya que necesitamos alguna magnitud que de cuenta de como está distribuida la masa alrededor de cierto punto o eje de rotación (por ejemplo un eje que pase por el centro de masa). Esa magnitud es el tensor de inercia que caracteriza la inercia rotacional del sólido.

Ese tensor de inercia sólido rígido se define como un tensor simétrico de segundo orden tal que la forma cuadrática construida a partir del tensor y la velocidad angular ω da la energía cinética de rotación, es decir:

(4) $E_{rot} = \frac{1}{2} \left( \begin{matrix} \omega_{x} & \omega_{y} & \omega_{z}\\ \end{matrix} \right) \left( \begin{matrix} I_{xx} & I_{xy} & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{zy} & I_{zz} \end{matrix} \right) \left( \begin{matrix} \omega_{x} \\ \omega_{y} \\ \omega_{z}\\ \end{matrix} \right) = \frac{1}{2} \sum_{j} \sum_{k} I_{jk} \omega_{j} \omega_{k}$

No sólo la energía cinética se puede expresar sencillamente en términos del tensor de inercia, si reescribimos la expresión (3) para el momento angular introduciendo en ella la definición del tensor de inercia, tenemos que este tensor es la aplicación lineal que relaciona la velocidad angular y el momento angular:

(5) $\mathbf{L}_G = \mathbf{I}\boldsymbol\omega = \left( \begin{matrix} I_{xx} & I_{xy} & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{zy} & I_{zz} \end{matrix} \right) \left( \begin{matrix} \omega_{x} \\ \omega_{y} \\ \omega_{z}\\ \end{matrix} \right)$

Ecuaciones del movimiento

Ángulos de Euler

Artículo principal: Ángulos de Euler

Los ángulos de Euler son tres coordenadas angulares que permiten relacionar la orientación de un sistema de ejes respecto a otro. En mecánica del sólido rígido se consideran normalmente dos sistemas de referencia: un sistema de ejes fijo o asociado a un observador inercial y otro móvil respecto al primero pero solidario con el sólido rígido. Aunque técnicamente es posible plantear las ecuaciones de Newton para el sistema inercial relacionando las magnitudes del sistema asociado al sólido rígido mediante la matriz de rotación asociada a los ángulos de Euler, resulta un sistema de ecuaciones poco práctico debido a que en ese sistema el tensor de inercia varía con el tiempo. Por otro lado, los ángulos de Euler proporcionan tres coordenadas generalizadas adecuadas para describir el movimiento de sólidos rígidos mediante los métodos de la mecánica lagrangiana.

Ecuaciones de Euler

Artículo principal: Ecuaciones de Euler (sólidos)

Cuando las ecuaciones del movimiento de un sólido rígido se expresan en un sistema de referencia no inercial solidario con los ejes principales de inercia del sólido rígido toman una fórmula particularmente simple conocida como ecuaciones de Euler. En general, en este sistema de referencia es mucho más sencillo integrar las ecuaciones de movimientos que en un sistema de referencia inercial y no solidario con el cuerpo. Las ecuaciones de Euler para el movimiento de un sólido rígido tienen la forma:

\begin{matrix} I_1\dot{\omega}_{1}+(I_3-I_2)\omega_2\omega_3 &=& M_{1}\\ I_2\dot{\omega}_{2}+(I_1-I_3)\omega_3\omega_1 &=& M_{2}\\ I_3\dot{\omega}_{3}+(I_2-I_1)\omega_1\omega_2 &=& M_{3} \end{matrix}

donde

M_{k} \,

son las componentes vectoriales del momento o torque total aplicado,

I_{k} \,

son los momentos principales de inercia y

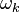\omega_{k}

son las componentes del vector velocidad angular

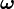\boldsymbol\omega

según los ejes principales de inercia.

Peonza simétrica

Se llama peonza simétrica a un sólido rígido de revolución, con dos de sus momentos de inercia principales iguales

I_1 = I_2 \ne I_3

. Como en una peonza simétrica se pueden escoger arbitrariamente los ejes 1 y 2, conviene aprovechar ese hecho para simplificar las expresiones tomando el eje 1 paralelo a la línea nodal de los ángulos de Euler lo cual equivale a que ψ = 0. Lo cual lleva a que las velocidades angulares en el sistema de referencia no inercial vengan dadas por:

\boldsymbol{\omega} = \begin{Bmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{Bmatrix} = \begin{Bmatrix} \dot\theta \\ \dot\phi \sin\theta \\ \dot\phi \cos\theta + \dot\psi \end{Bmatrix}

La energía cinética de rotación una peonza simétrica puede expresarse en términos de los ángulos de Euler sencillamente:

E_c = \frac{1}{2}\left(I_1 \omega_1^2 + I_1 \omega_2^2 + I_3 \omega_3^2\right)= \frac{I_1}{2}\left(\dot\phi^2 \sin^2\theta + \dot\theta^2\right) + \frac{I_3}{2}\left(\dot\phi \cos\theta + \dot\psi\right)^2

Por otro lado si se toma el eje Z del sistema de referencia alineado con el momento angular del sólido rígido se tiene que las componentes del momento angular y la relación con la velocidad angular son:

\mathbf{M}=\begin{Bmatrix} 0 \\ M\sin \theta \\ M\cos \theta \end{Bmatrix} = \begin{bmatrix} I_1 & 0 & 0 \\ 0 & I_1 & 0 \\ 0 & 0 & I_3 \end{bmatrix} \begin{Bmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{Bmatrix} = \begin{Bmatrix} I_1\dot\theta \\ I_1\dot\phi \sin\theta \\ I_3\dot\phi \cos\theta + \dot\psi \end{Bmatrix}

Escribiendo componente a componente estas ecuaciones se tiene que:

\dot\theta = 0 \qquad I_1\dot\phi = M \qquad I_3\omega_3 = I_3(\dot\phi \cos\theta + \dot\psi) = M \cos \theta

La primera ecuación nos dice que en el movimiento libre de una peonza simétrica esta no cabecea, es decir, no hay movimiento de nutación ya que el ángulo formado por eje de rotación y el momento angular se mantiene constante en el movimiento. La segunda describe el movimiento de precesión de acuerdo con el cual el eje de rotación (que coincide con la dirección de la velocidad angular) gira alrededor de la dirección del momento angular (eje Z). La tercera ecuación da la velocidad de rotación del sólido alrededor de su tercer eje de inercia.

Peonza asimétrica

Una peonza asimétrica es un sólido rígido tal que ninguno de sus tres momentos principales de inercia tiene el mismo valor, es común nombrarlos en orden ascendente como:

I_1 < I_2 < I_3

. En el movimiento de giro libre de una peonza tiene dos integrales de movimiento:

(6a) $\frac{L_1^2}{I_1}+\frac{L_2^2}{I_2}+\frac{L_3^2}{I_3} = 2E \;$

(6b) $L_1^2 + L_2^2 + L_3^2 = L^2 \;$

Como sólo existen tres coordenadas angulares y existen esas dos restricciones las componentes del momento angular sólo pueden variar a lo largo de una curva dada por la intersección del elipsoide (6a) y la esfera (6b). Así mismo puede verse que el giro alrededor de los ejes de inercia asociado a los momentos

I_1, I_3

es estable mientras que el asociado a

I_2

es inestable, es decir, cualquier pequeña perturbación cambia drásticamente las trayectorias del movimiento. Para

L^2 > 2EI_2

las ecuaciones paramétricas de variación de las velocidades angulares vienen dadas por las funciones elípticas de Jacobi:

\omega_1 = \sqrt{\frac{2EI_3-L^2}{I_1(I_3-I_1)}} \mbox{cn} \tau

\omega_2 = \sqrt{\frac{2EI_3-L^2}{I_1(I_3-I_2)}} \mbox{sn} \tau

\omega_3 = \sqrt{\frac{L^2-2EI_1}{I_1(I_3-I_2)}} \mbox{dn} \tau

con:

\tau = t \sqrt{\frac{(I_3-I_2)(L^2-2EI_1)}{I_1I_2I_3}}

L^2 < 2EI_2

basta intercambiar los subíndices 1 y 3 en las anteriores expresiones.
Finalmente conviene observar que cuando

I_1 \to I_2

las funciones elípticas de Jacobi se reducen a funciones trigonométricas ordinarias, y las ecuaciones del movimiento se reducen a las de una peonza simétrica:

\mbox{sn} \tau \to \sin \tau, \quad \mbox{cn} \tau \to \cos \tau, \quad \mbox{dn} \tau \to 1

Principio del trabajo virtual

Véase también: Principio de los trabajos virtuales

El principio del trabajo virtual establece que si un cuerpo está en equilibrio, entonces la suma algebraica del trabajo virtual realizado por todas las fuerzas y los momentos de par que actúan sobre el cuerpo, es cero para cualquier desplazamiento virtual del cuerpo.¹

Sólido rígido en mecánica cuántica

Artículo principal: Rotor rígido

La formulación cuántica se realiza mediante la cuantización de la variedad simpléctica 12-dimensional asociada a un sólido rígido. El espacio de configuración de un sólido rígido es SO(3) x R³ y por tanto un espacio de Hilbert adecuado para el sólido rígido es isomorfo al producto tensorial de espacios de funciones de cuadrado integrable

L^2(SO(3),\mu_H)\otimes L^2(\R^3,\mu_L)

, donde

\mu_H,\ \mu_L\;

son respectivamente la medida de Haar de SO(3) y la medida de Lebesgue de R³.
Dada la compacidad de SO(3), la energía cinética de rotación puede considerarse como una suma directa de operadores actuando sobre espacios vectoriales de dimensión finita.

tipos de movimiento